Density functional perturbation theory for phonon calculations
In the past, I sticked to finite displacement method to calculate
phonon dispersion thanks to the excellent implementation of
ALAMODE. Also, direct calculations in real space are
intuitive and straightforward. However, due to recent interest in the
phonon-electron interaction which necessitates the calculations of
deformation potential, DFPT is a must. In this post, I will try to learn
the theory and practice of DFPT in phonon calculations.
Basic formalisms of DFT and DFPT
Density functional theory (DFT)
Generally, DFT solves the many-body Schrödinger equation by introducing the electron density as the basic variable. The original equation is,
\[ \begin{aligned} \Bigg\lbrace -\sum_i \frac{\hbar^2}{2m_e} \nabla_i^2 &- \sum_I \frac{\hbar^2}{2M_I}\nabla_I^2 + \frac{1}{2}\sum_{i\neq j} \frac{e^2}{4\pi\epsilon_0} \frac{1}{|\hat{\boldsymbol{r}}_i - \hat{\boldsymbol{r}}_j|} \\ &+ \frac{1}{2}\sum_{I\neq J}\frac{e^2}{4\pi\epsilon_0} \frac{Z_I Z_J}{|\hat{\boldsymbol{R}}_I - \hat{\boldsymbol{R}}_J|} - \sum_{i, I}\frac{e^2}{4\pi\epsilon_0}\frac{Z_I}{|\hat{\boldsymbol{r}}_i - \hat{\boldsymbol{R}}_I|}\Bigg\rbrace \boldsymbol{\Psi} = E_{\text{tot}} \boldsymbol{\Psi}. \end{aligned} \]
It is thus impossible to solve the equation exactly. Since the electronic sturcture is the main interest, a convinent approach is to introduce Born-Oppenheimer approximation, that is, nuclei and electrons are treated separately. In our case, the nuclei are fixed at their equilibrium positions (or any other given positions), the wavefunction is thus a function of electron coordinates only. Another approximation is to assume that the wavefunction can be written as a product of single-electron wavefunctions, that is,
\[ \boldsymbol{\Psi} (\boldsymbol{r}_1, \cdots, \boldsymbol{r}_N) = \prod_i \psi_i(\boldsymbol{r}_i), \]
or,
\[ \ket{\Psi} = \ket{\psi_1}\otimes\ket{\psi_2}\otimes\cdots\otimes\ket{\psi_N}, \]
where \(\boldsymbol{r}_i\) is the position of the \(i\)-th electron (note that the symbol \(\boldsymbol{r}_i\) and \(\hat{\boldsymbol{r}}\): here, it is the coordinate, while in the previous many-body Schrödinger equation, it was the position operator). Also, with this assumption, keep in mind that the system under investigation should be a weakly correlated system, that is the electron-electron interaction is weak.
Those assumptions are not enough to make the problem tractable, since the original equation still cannot be decomposed into several single-electron equations due to the electron-electron interaction term. To solve this problem, mean-field approximation is introduced, to replace the electron-electron interaction term by the combination of the electron-electron Coulomb energy and the electron-electron exchange energy (which is resulted by the Pauli exclusion principle). In short, if we denote the charge density as \(n(\boldsymbol{r})\), the Coulomb potential is:
\[ V^{\text{H}} = \frac{e^2}{4\pi\epsilon_0} \int \frac{n(\boldsymbol{r}')}{|\boldsymbol{r} - \boldsymbol{r}'|} \mathrm{d}\boldsymbol{r}'. \]
Here, the superscript H stands for Hartree. The exchange potential is denoted by \(V^{\text{xc}}(n) = \delta E_{\text{xc}}/\delta n\), and is approximated by approaches like LDA, GGA, etc, and we won't cover them here. Applying all above approximations, the final equation (Kohn-Sham equation) is:
\[ \Big[\underbrace{-\frac{\hbar^2}{2m_e}\nabla^2 + V^{\text{tot}}(\boldsymbol{r})}_{\hat{H}^{\text{KS}}}\Big]\psi_i (\boldsymbol{r}) = \epsilon_i \psi_i (\boldsymbol{r}), \]
with:
\[ \begin{alignedat}{2} V^{\text{tot}}(\boldsymbol{r}) &= V^{\text{n}} (\boldsymbol{r}) + V^{\text{H}}(\boldsymbol{r}) + V^{xc}(\boldsymbol{r}), \\ V^{\text{n}}(\boldsymbol{r}) &= -\sum_I \frac{Z_I e^2}{4\pi\epsilon_0 |\boldsymbol{r} - \boldsymbol{R}_I|}, && \text{(nucleus-electron)} \\ V^{\text{H}}(\boldsymbol{r}) &= \frac{e^2}{4\pi\epsilon_0} \int \frac{n(\boldsymbol{r}')}{|\boldsymbol{r} - \boldsymbol{r}'|} \mathrm{d}\boldsymbol{r}', && \text{(Hatree)} \\ V^{\text{xc}}(\boldsymbol{r}) &= \frac{\delta E_{\text{xc}}}{\delta n(\boldsymbol{r})} && \text{(exchange-correlation)}. \end{alignedat} \]
And the most important thing is that the charge density \(n(\boldsymbol{r})\) is determined by the wavefunctions \(\psi_i(\boldsymbol{r})\):
\[ n(\boldsymbol{r}) = \sum_{\text{occupied }i} |\psi_i(\boldsymbol{r})|^2. \]
The advantage of this formulation is that the solution can be obtained self-consistently. One comes up with an initial guess of the charge density \(n\), then solve the Kohn-Sham equation to get a series of wavefunctions \(\psi_i\) for each \(\boldsymbol{k}\) point. Then, calculate the charge density \(n\) from the wavefunctions, and compare it with the initial guess. If they are not the same, update the charge density and solve the Kohn-Sham equation again. This process is repeated until the charge density converges.
Density functional perturbation theory (DFPT)
DFPT is a method to calculate the response of the system to external perturbations, and one direct application is the phonon calculations, where the system is perturbed by atomic displacements. The first-order variation of the Kohn-Sham equation is easilly obtained as:
\[ \Big[\hat{H}^{\text{KS}} - \epsilon_i \Big] \Delta\psi_i (\boldsymbol{r}) = (\Delta \epsilon_i - \Delta V^{\text{tot}}(\boldsymbol{r})) \psi_i (\boldsymbol{r}). \]
Like DFT, the perturbation of the charge density \(\Delta n(\boldsymbol{r})\) also plays a vital role in solving the perturbed Kohn-Sham equation. It can be derived from the expression of \(V^{\text{tot}}\) that,
\[ \begin{aligned} \Delta V^{\text{tot}}(\boldsymbol{r}) &= \Delta V^{\text{n}}(\boldsymbol{r}) + \Delta V^{\text{H}}(\boldsymbol{r}) + \Delta V^{xc}(\boldsymbol{r}) \\ \Delta V^{\text{H}}(\boldsymbol{r}) &= \frac{e^2}{4\pi \epsilon_0} \int \frac{\Delta n(\boldsymbol{r}')}{|\boldsymbol{r} - \boldsymbol{r}'|} \mathrm{d}\boldsymbol{r}', \\ \Delta V^{xc}(\boldsymbol{r}) &= \frac{\mathrm{d}}{\mathrm{d}n} \Bigg(\frac{\delta E_{\text{xc}}}{\delta n}\Bigg) \Delta n(\boldsymbol{r}). \end{aligned} \]
\(V^n\) is usually supplied externally, for example, the atomic positions are perturbed. The perturbation of the charge density is
\[ \Delta n(\boldsymbol{r}) = 2\mathrm{Re}\Big(\sum_{\text{occupied }i}\psi_i(\boldsymbol{r})^* \Delta \psi_i(\boldsymbol{r})\Big) \]
For a perturbation factor \(\lambda\), all the perturbed quantities can be expressed in the form of \(\frac{\partial}{\partial \lambda}\), but we won't bother to write the equations again. Finally, we see that the perturbed Kohn-Sham equation can also be solved self-consistently.
However, the only problem that remains is the singularity lying on the left-hand side of the perturbed Kohn-Sham equation, making the solution to \(\Delta \psi_i\) not unique. To solve this, we first take a look at the analytical expression for \(\Delta\psi_i\). Multiplying the basis decomposition \(\sum_j \ket{\psi_j}\bra{\psi_j}\) to the perturbed Kohn-Sham equation, we can solve that,
\[ \braket{\psi_j|\Delta\psi_i} = \frac{\braket{\psi_j | \Delta V^{\text{tot}} | \psi_i}}{\epsilon_i - \epsilon_j} \quad \text{for } i \neq j. \]
Since \(\psi_j\) constitutes a complete set of basis, the perturbed wavefunction can thus be expressed as a linear combination, in which the coefficients are determined by the above equation. The charge density is thus rewritten as
\[ \begin{aligned} \Delta n = 2\mathrm{Re} \sum_{\text{occupied }i} \sum_{j\neq i} \left(\psi_i^* \psi_j \frac{\braket{\psi_j | \Delta V^{\text{tot}} | \psi_i}}{\epsilon_i - \epsilon_j} \right) \end{aligned} \]
Note that \(j\) runs over all states no matter whether they are occupied or not in the whole Brillouin zone. It can be seen that the contributions from the occupied states to the charge density cancel each other, and thus the singularity can be removed if we project the perturbed wavefunctions to the unoccupied states:
\[ \Big[\hat{H}^{\text{KS}} - \epsilon_i \Big] P_c \ket{\Delta\psi_i} = - P_c \Delta V^{\text{tot}} \ket{\psi_i} \]
with \(P_c\) denoting the projection operator to the unoccupied states:
\[ P_c = \sum_{\text{unoccupied }j} \ket{\psi_j}\bra{\psi_j} = 1 - \sum_{\text{occupied }j} \ket{\psi_j}\bra{\psi_j}. \]
From the projected equation, once the trail solution to the perturbed wavefunction is chosen on the unoccupied states basis, the singularity is removed, and the iteration process will still keep this orthogonality.
Phonon calculations
Phonon is the quantized lattice vibration due to the ion displacements. Starting from the Born-Oppenheimer approximation, the Schrödinger equation for the ions is:
\[ \Bigg[-\sum_I \frac{\hbar^2}{2M_I}\frac{\partial^2}{\partial \boldsymbol{R}_I^2} + E(\boldsymbol{R})\Bigg] \Phi(\boldsymbol{R}) = \mathcal{E} \Phi(\boldsymbol{R}). \]
Here, \(E(\boldsymbol{R})\) is the ground state energy of the system with fixed ion positions \(\boldsymbol{R}\). This energy could be obtained by the electronic structure calculations with the Hamiltonian parameterized by \(\boldsymbol{R}\):
\[ \begin{aligned} \hat{H}_{\text{BO}} (\boldsymbol{R}) = & -\sum_i\frac{\hbar^2}{2m_e} \nabla_i^2 + \frac{1}{2} \sum_{i\neq j} \frac{e^2}{4\pi\epsilon_0} \frac{1}{|\boldsymbol{r}_i - \boldsymbol{r}_j|} \\ & \underbrace{- \sum_{i, I} \frac{e^2}{4\pi\epsilon_0} \frac{Z_I}{|\boldsymbol{r}_i - \boldsymbol{R}_I|}}_{V_{\boldsymbol{R}}(\boldsymbol{r})} + \underbrace{\frac{1}{2} \sum_{I\neq J} \frac{e^2}{4\pi\epsilon_0} \frac{Z_I Z_J}{|\boldsymbol{R}_I - \boldsymbol{R}_J|}}_{E_N(\boldsymbol{R})}. \end{aligned} \]
Notice that this Hamiltonian is the exact Hamiltonian after the Born-Oppenheimer approximation, and the Hamiltonian \(H_{\text{KS}}\) in the DFT calculations is an approximation to this one with modified electron-electron interaction terms. Also, the ion-ion interaction term is neglected in \(H_{\text{KS}}\) since it is not relevant to the electronic structure.
As discussed in the previous post, the term \(E(\boldsymbol{R})\) should be expanded in a Taylor series around the equilibrium positions. For the second-order approximation, we seek the derivative \(\partial^2 E/\partial R_{I\alpha} \partial R_{J\beta}\), i.e. the harmonic force constant labeled by \(I\alpha J\beta\):
\[ \begin{aligned} \frac{\partial^2 E}{\partial R_{I\alpha} \partial R_{J\beta}} &= \frac{\partial}{\partial R_{J\beta}} \Braket{\psi | \frac{\partial \hat{H}_{\text{BO}}}{\partial R_{I\alpha}} | \psi} \\ &= \Braket{\psi | \frac{\partial^2 \hat{H}_{\text{BO}}}{\partial R_{I\alpha} \partial R_{J\beta}} | \psi} + 2 \mathrm{Re} \Bigg(\Braket{\psi | \frac{\partial \hat{H}_{\text{BO}}}{\partial R_{I\alpha}} | \frac{\partial \psi}{\partial R_{J\beta}} }\Bigg). \end{aligned} \]
Here, \(\psi\) is the electronic wavefunction corresponding to \(\hat{H}_{\text{BO}}\). The first line of the above equation is due to the Hellmann-Feynman theorem, and the second line is derived by the chain rule. In fact, the only terms in \(\hat{H}_{\text{BO}}\) that explicitly depend on \(\boldsymbol{R}\) are the ion-electron interaction \(V_{\boldsymbol{R}}\) and ion-ion interaction \(E_N\) terms. This second derivative can be also expressed by the charge density to eliminate the wavefunction:
\[ \frac{\partial^2 E}{\partial R_{I\alpha}\partial R_{J\beta}} = \int \frac{\partial n (\boldsymbol{r})}{\partial R_{J\beta}}\frac{\partial V_{\boldsymbol{R}}}{\partial R_{I\alpha}} \mathrm{d}\boldsymbol{r} + \int n(\boldsymbol{r}) \frac{\partial^2 V_{\boldsymbol{R}}}{\partial R_{I\alpha}\partial R_{J\beta}} \mathrm{d}\boldsymbol{r} + \frac{\partial^2 E_N}{\partial R_{I\alpha}\partial R_{J\beta}}. \]
Since \(V_{\boldsymbol{R}}\) and \(E_N\) are known, it is thus clear that \(n(\boldsymbol{r})\) and \(\partial n(\boldsymbol{r})/\partial R_{I\alpha}\) are needed, and they should be able to be calculated by DFT and DFPT, respectively.
Instead of \(I, J\), we now represent atoms by their unit cell vector \(\boldsymbol{l}\), and the atom position vector \(\boldsymbol{b}\) within the unit cell. For each atom, the displacement is thus denoted by \(u_{\alpha}(\boldsymbol{l}\boldsymbol{b})\). Using the plane-wave basis, that the atoms are displaced by \(u_{\alpha}(\boldsymbol{l}\boldsymbol{b}) = U_{\alpha}(\boldsymbol{q}\boldsymbol{b}) e^{i\boldsymbol{q}\cdot\boldsymbol{l}}\), the dynamical matrix introduced in the previous post can be written as:
\[ \begin{aligned} D_{\alpha\beta}(\boldsymbol{b}\boldsymbol{b}'|\boldsymbol{q}) &= \frac{1}{\sqrt{M_{\boldsymbol{b}}M_{\boldsymbol{b}'}}} \sum_{l'} \frac{\partial^2 E}{\partial u_{\alpha}(\boldsymbol{0}\boldsymbol{b}) \partial u_{\beta}(\boldsymbol{l'}\boldsymbol{b}')} e^{i\boldsymbol{q}\cdot\boldsymbol{l}'} = \frac{1}{N_p \sqrt{M_{\boldsymbol{b}}M_{\boldsymbol{b}'}}} \frac{\partial^2 E}{\partial U^*_{\alpha}(\boldsymbol{q}\boldsymbol{b}) \partial U_{\beta}(\boldsymbol{q}\boldsymbol{b}')}\\ &= \frac{1}{N_p\sqrt{M_{\boldsymbol{b}}M_{\boldsymbol{b}'}}} \int \left(\frac{\partial n(\boldsymbol{r})}{\partial U_\alpha (\boldsymbol{q}\boldsymbol{b})}\right)^* \frac{\partial V_{\boldsymbol{R}}(\boldsymbol{r})}{\partial U_{\beta} (\boldsymbol{q}\boldsymbol{b}')}\mathrm{d}r + \ \text{explicit}\ \text{terms} \end{aligned} \]
Besides the explicit terms (see Baroni's 2001 Rev Mod Phys), it can be seen that only the perturbed charge density is required to calculate the dynamical matrix. Therefore, with a given phonon wavevector \(\boldsymbol{q}\), the response of the charge density to all \(3N\) (where \(N\) is the number of atoms in the unit cell) degrees of freedom should be calculated. \(\forall \alpha, \boldsymbol{b}\), due to that the periodicity of \(\Delta V^{\text{tot}}\) alignes with the monochromatic perturbation \(U_\alpha (\boldsymbol{q}\boldsymbol{b})\), i.e., it can be written that,
\[ \Delta V^{\text{tot}}_{\boldsymbol{q}\boldsymbol{b}\alpha}(\boldsymbol{r}) = \Delta v^{\text{tot}}_{\boldsymbol{q}\boldsymbol{b}\alpha}(\boldsymbol{r}) e^{i\boldsymbol{q}\cdot\boldsymbol{r}}, \]
where \(\Delta v^{\boldsymbol{q}}(\boldsymbol{r})\) is periodic across unit cells. Now we look back at the perturbed Kohn-Sham equation:
\[ \Big[\hat{H}^{\text{KS}} - \epsilon_i \Big] P_c \ket{\Delta\psi_{i, \boldsymbol{q}\boldsymbol{b}\alpha}} = - P_c \Delta V^{\text{tot}}_{\boldsymbol{q}\boldsymbol{b}\alpha} \ket{\psi_i}. \]
Assume that this state \(i\) pocesses electron wavevector \(\boldsymbol{k}_i\), we can read from the right-hand side that the perturbation \(\ket{\Delta\psi_{i, \boldsymbol{q}\boldsymbol{b}\alpha}}\) should be a periodic function times \(e^{i(\boldsymbol{q}+\boldsymbol{k}_i)\cdot \boldsymbol{r}}\) (\(\boldsymbol{q}\) comes from \(\Delta V^{\text{tot}}_{\boldsymbol{q}\boldsymbol{b}\alpha}\), while \(\boldsymbol{k}_i\) comes from \(\ket{\psi_i}\)). Therefore, \(\ket{\Delta \psi_{i,\boldsymbol{q}\boldsymbol{b}\alpha}}\) can be directly solved by using the unoccupied states basis at \(\boldsymbol{k}_i+\boldsymbol{q}\).
The DFPT procedure for phonon calculations is thus clear: given phonon wavevector \(\boldsymbol{q}\), for each occupied electron state, we solve the perturbed Kohn-Sham equation \(3N\) times for different monochromatic perturbations to obtain the perturbed wavefunction and charge density. Then the dynamical matrix can be calculated by using all the perturbed charge densities. Once the dynamical matrix is obtained, the phonon frequencies can be calculated by diagonalizing it (see the previous post).
Here, I calculated the phonon dispersion of silicon using the finite
displacement method and DFPT. The former is performed by
ALAMODE with Quantum ESPRESSO as the DFT
backend, while the latter is performed by ph.x in
Quantum ESPRESSO. The phonon dispersion is shown below:
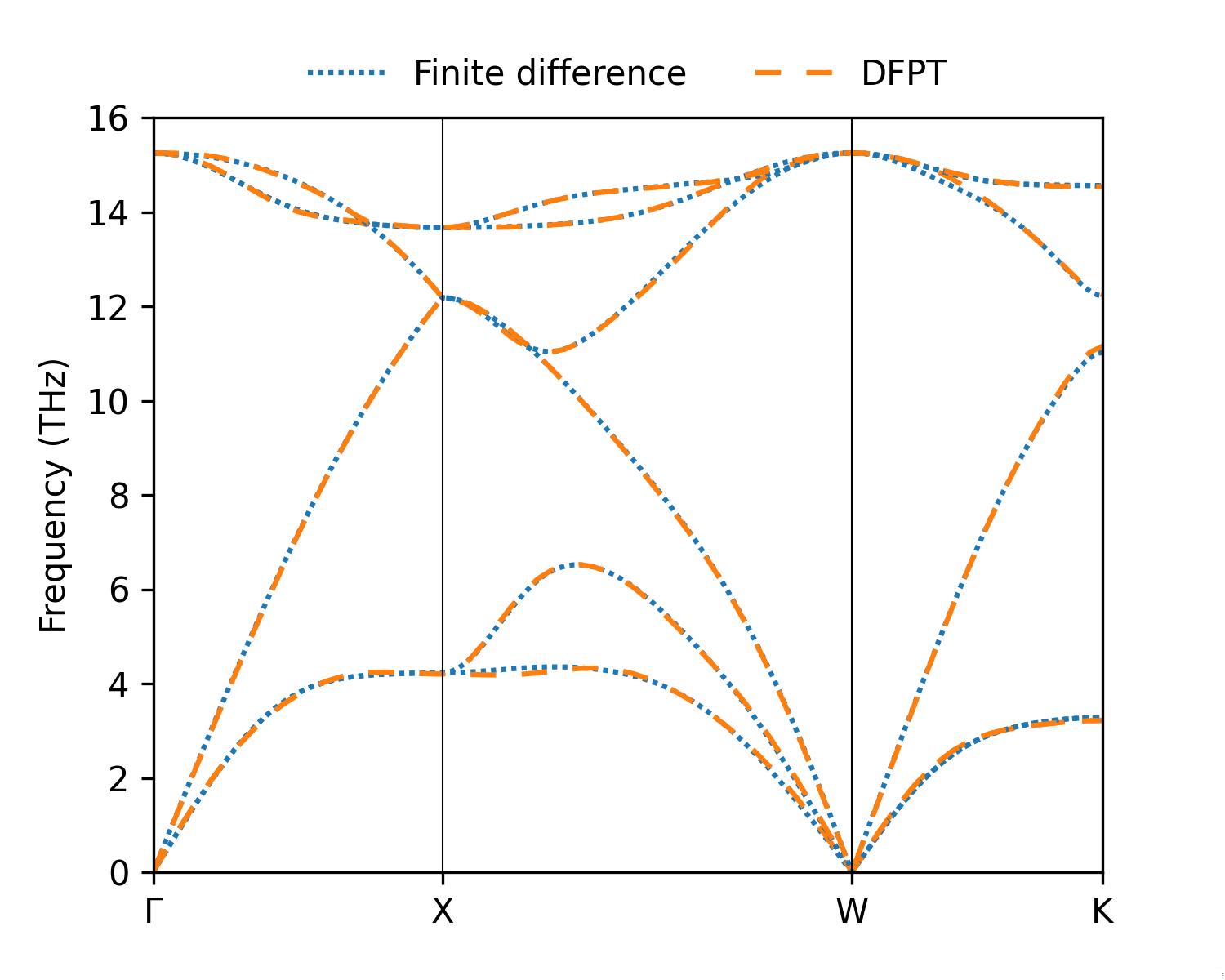
Phonon-electron coupling
From the above formulation, it can be seen that, for an electron with wavevector \(\boldsymbol{k}_i\), the perturbed wavefunction in response to the monochromatic perturbation \(\boldsymbol{q}\) has the wavevector \(\boldsymbol{k}_i + \boldsymbol{q}\). This fact hints the phonon-electron coupling. The electron-phonon interaction (EPI) Hamiltonian can be understood as the perturbation to the Kohn-Sham Hamiltonian due to the atomic displacements, that is,
\[ \hat{H}_{\text{ep}} = \sum_{\boldsymbol{l}\boldsymbol{b}\alpha} \frac{\partial V^{\text{tot}}}{\partial u_{\alpha}(\boldsymbol{l}\boldsymbol{b})}\Big|_{0} u_{\alpha}(\boldsymbol{l}\boldsymbol{b}). \]
In the previous post, we have defined the following transformations:
\[ \begin{aligned} &\left\lbrace \begin{aligned} \boldsymbol{X}(\boldsymbol{q}\boldsymbol{b}) &= \frac{1}{\sqrt{N_p}} \sum_{\boldsymbol{l}} \boldsymbol{u}(\boldsymbol{l}\boldsymbol{b}) e^{-i \boldsymbol{q}\cdot\boldsymbol{l}}, \\ \boldsymbol{P}(\boldsymbol{q}\boldsymbol{b}) &= \frac{1}{\sqrt{N_p}} \sum_{\boldsymbol{l}} \boldsymbol{p}(\boldsymbol{l}\boldsymbol{b}) e^{i \boldsymbol{q}\cdot\boldsymbol{l}}, \end{aligned} \right. \\ &\left\lbrace \begin{aligned} \boldsymbol{X}(\boldsymbol{q}s) &= \sum_{\boldsymbol{b}} \sqrt{m_{\boldsymbol{b}}} \boldsymbol{e}^* (\boldsymbol{b}| \boldsymbol{q}s) \boldsymbol{X}(\boldsymbol{q}\boldsymbol{b}), \\ \boldsymbol{P}(\boldsymbol{q}s) &= \sum_{\boldsymbol{b}} \sqrt{\frac{1}{m_{\boldsymbol{b}}}} \boldsymbol{e} (\boldsymbol{b}| \boldsymbol{q}s) \boldsymbol{P}(\boldsymbol{q}\boldsymbol{b}), \end{aligned} \right. \\ &\left\lbrace \begin{aligned} \hat{a}_{\boldsymbol{q}s} &= \frac{1}{\sqrt{2\hbar\omega (\boldsymbol{q}s)}} \boldsymbol{P}(\boldsymbol{q}s) - i \sqrt{\frac{\omega (\boldsymbol{q}s)}{2\hbar}} \boldsymbol{X}^{\dagger} (\boldsymbol{q}s), \\ \hat{a}_{\boldsymbol{q}s}^{\dagger} &= \frac{1}{\sqrt{2\hbar\omega (\boldsymbol{q}s)}} \boldsymbol{P}^{\dagger}(\boldsymbol{q}s) + i \sqrt{\frac{\omega (\boldsymbol{q}s)}{2\hbar}} \boldsymbol{X} (\boldsymbol{q}s). \end{aligned} \right. \end{aligned} \]
Step by step, the EPI Hamiltonian can be expressed by the phonon creation and annihilation operators:
\[ \begin{aligned} \hat{H}_{\text{ep}} &= \sum_{\boldsymbol{q}s} \sum_{\boldsymbol{l}\boldsymbol{b}\alpha} \frac{-i}{\sqrt{N_p m_{\boldsymbol{b}}}} \sqrt{\frac{\hbar}{2\omega (\boldsymbol{q}s)}} \frac{\partial V^{\text{tot}}}{\partial u_{\alpha}(\boldsymbol{l}\boldsymbol{b})}\Big|_{0} e_{\alpha} (\boldsymbol{b}| \boldsymbol{q}s) e^{i\boldsymbol{q}\cdot \boldsymbol{l}} (\hat{a}_{\boldsymbol{q}s}^{\dagger} - \hat{a}_{-\boldsymbol{q}s}) \\ &=\sum_{\boldsymbol{q}s} e^{i\boldsymbol{q}\cdot \boldsymbol{r}} \underbrace{\sum_{\boldsymbol{b}\alpha} \frac{-i}{\sqrt{N_p m_b}} \sqrt{\frac{\hbar}{2\omega (\boldsymbol{q}s)}} \frac{\partial v^{\text{tot}}_{\boldsymbol{q}\boldsymbol{b}\alpha}}{\partial U_{\alpha} (\boldsymbol{q}\boldsymbol{b})} e_{\alpha} (\boldsymbol{b}| \boldsymbol{q}s)}_{\Delta_{\boldsymbol{q}s}v^{\text{tot}}} (\hat{a}_{\boldsymbol{q}s}^{\dagger} - \hat{a}_{-\boldsymbol{q}s})\\ &= \sum_{\boldsymbol{q}s} e^{i\boldsymbol{q}\cdot \boldsymbol{r}} \Delta_{\boldsymbol{q}s}v^{\text{tot}} (\hat{a}_{\boldsymbol{q}s}^{\dagger} - \hat{a}_{-\boldsymbol{q}s}). \end{aligned} \]
The second line replaced \(\sum_{\boldsymbol{l}}\frac{\partial}{\partial u_\alpha (\boldsymbol{l}\boldsymbol{b})}e^{i\boldsymbol{q}\cdot\boldsymbol{l}}\) by the derivative with respect to \(U_{\boldsymbol{\alpha}}(\boldsymbol{q}\boldsymbol{b})\). Also, we have used the property that the perturbated potential should be a periodic function across the unit cell times \(e^{i\boldsymbol{q}\cdot\boldsymbol{r}}\). By using the second quantization on the Fock space, the EPI Hamiltonian is decomposed into the electron creation and annihilation operators basis:
\[ \begin{aligned} \hat{H}_{\text{ep}} &= \sum_{\boldsymbol{q}s} \sum_{\boldsymbol{k}_i, \boldsymbol{k}_j} \Braket{\psi_{\boldsymbol{k}_i} | \Delta_{\boldsymbol{q}s}v^{\text{tot}} e^{i\boldsymbol{q}\cdot \boldsymbol{r}} | \psi_{\boldsymbol{k}_j}} (\hat{a}_{\boldsymbol{q}s}^{\dagger} - \hat{a}_{-\boldsymbol{q}s}) c_{\boldsymbol{k}_i}^{\dagger} c_{\boldsymbol{k}_j} \\ &= \sum_{\boldsymbol{q}s} \sum_{\boldsymbol{k}} \Braket{\psi_{\boldsymbol{k}+\boldsymbol{q}} | \Delta_{\boldsymbol{q}s}v^{\text{tot}} e^{i\boldsymbol{q}\cdot \boldsymbol{r}} | \psi_{\boldsymbol{k}}} (\hat{a}_{\boldsymbol{q}s}^{\dagger} - \hat{a}_{-\boldsymbol{q}s}) c_{\boldsymbol{k}+\boldsymbol{q}}^{\dagger} c_{\boldsymbol{k}}. \end{aligned} \]
Therefore, we could see that each term inside the summation represents two processes:
\[ \begin{aligned} \text{electron}_\boldsymbol{k} + \text{phonon}_{\boldsymbol{q}} &\rightarrow \text{electron}_{\boldsymbol{k}+\boldsymbol{q}}\\ \text{electron}_{\boldsymbol{k}} &\rightarrow \text{electron}_{\boldsymbol{k}+\boldsymbol{q}} + \text{phonon}_{-\boldsymbol{q}}. \end{aligned} \]
Thus, the scattering rate could be calculated by Fermi's golden rule.
References
- Stefano Baroni, Stefano de Gironcoli, Andrea Dal Corso, and Paolo Giannozzi, Rev. Mod. Phys. 73, 515 (2001). DOI: 10.1103/RevModPhys.73.515
- Feliciano Giustino, Rev. Mod. Phys. 89, 015003 (2017). DOI: 10.1103/RevModPhys.89.015003
- Gyaneshwar P. Srivastava, Physics of Phonons, 2nd ed. (CRC Press, 2022).
- EPW summer school 2024.